THIS ARTICLE/PRESS RELEASE IS PAID FOR AND PRESENTED BY The Centre for Advanced Study (CAS) - read more

Real structures in tropical geometry.

Tropical geometry – a two-way bridge between mathematical fields

Meet the Young CAS Fellows for 2021-23: Kristin Shaw.

Adviser
Presented by: The Centre for Advanced Study

Kristin Shaw is an associate professor of mathematics at the University of Oslo (UiO) and will lead the Young CAS Fellow project Real Structures in Discrete, Algebraic, Symplectic, and Tropical Geometries (REACTIONS).

Tropical geometry is a relatively new field that can be described as a two-way bridge between mathematical fields: “Tropical geometry provides a bridge between the discrete world and the algebraic and symplectic ones, and ideas flow over this bridge in both directions,” Shaw said.

Shaw applied for the Young CAS Fellow programme because of its focus on collaboration.

“Many programs for young researchers focus on boosting an individual's body of work, when in reality we rarely work alone, even when we publish solo-authored papers,” Shaw said.

The project is one of the four Young CAS Fellow projects due to start in August 2021. The projects will last for two years.

Kristin Shaw, associate professor of mathematics at the University of Oslo (UiO),

We spoke with Shaw about the project and about having been selected for the Young CAS Fellow programme for 2021-23.

Congratulations! Could you briefly tell us about your project?

Thank you!

Algebra is a very rigid subject; it is full of rules, symbols and equalities. Topology literally means the study of space. Though, unlike geometry, topology isn't concerned with distance, angles and curvature. Its focus is connectedness, holes and how spaces intersect. It's helpful to think that a topologist basically works with spaces made out of rubber. Many deep, open problems in mathematics at their heart ask about the difference between rigid algebra and flexible topology.

Algebraic geometry deals with the shapes of solution sets to polynomial equations. The numbers that we allow as the solutions to these equations influence greatly the shapes that are obtained. For example, lines and circles are defined by equations, and when we draw their graphs we do so over real numbers. But most mathematicians prefer to work with complex numbers, which include the imaginary number √-1, and practically nothing is known about the shapes or ‘topology’ of solution sets of polynomial equations over the real numbers.

One aim of the project Real Structures in Discrete, Algebraic, Symplectic, and Tropical Geometries (REACTIONS) is to use relatively new tools from discrete and tropical geometries to investigate the topology of spaces arising from real algebraic equations and spaces in the so-called symplectic world. These types of applications can be traced back to the roots of tropical geometry, though there is hope that new techniques which have emerged can have a powerful impact.

Tropical geometry is a relatively new field arising out of the ideas of computer scientist Imre Simon, who developed the first ideas while working in Brazil. Tropical geometry provides a bridge between the discrete world and the algebraic and symplectic ones, and ideas flow over this bridge in both directions.

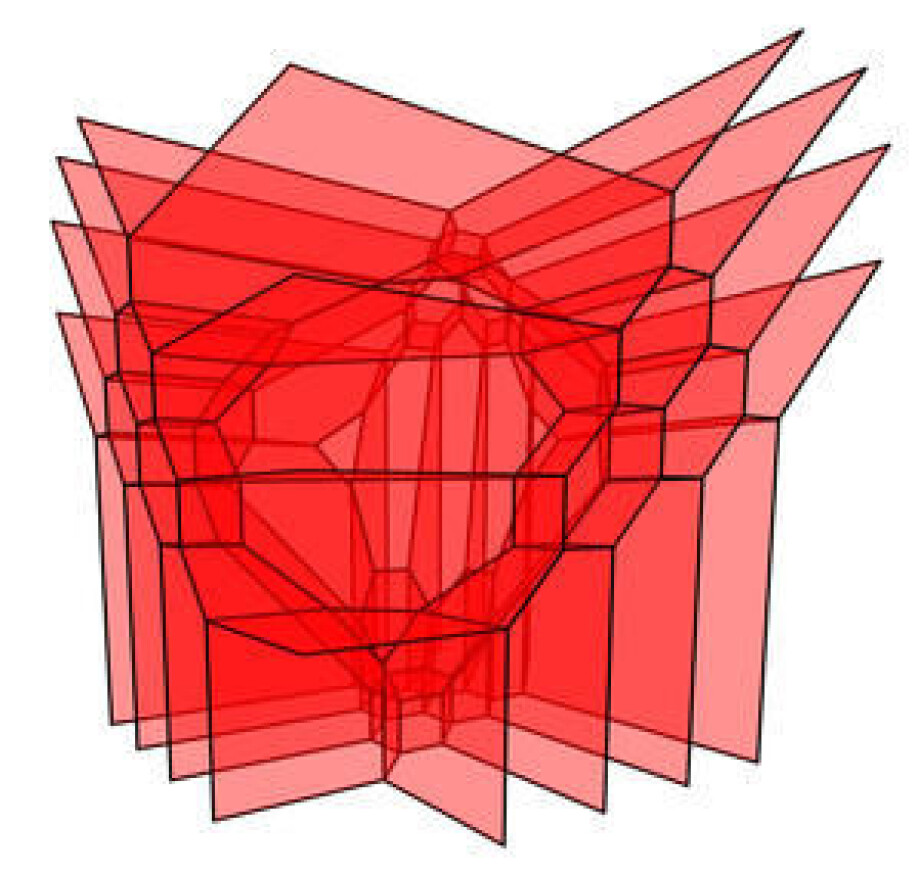
Another focus of this Young CAS Fellow project will be to utilise algebraic and symplectic techniques to provide new insights into axiomatic real structures arising in discrete mathematics, known as oriented matroids.

Please tell us about yourself, your research interests and your career path.

Before starting the position at the University of Oslo, I held a postdoc fellowships at the University of Toronto and the Fields Institute in Toronto. Later I was a Humboldt Postdoc Fellowship at the TU Berlin and a researcher at the Max Planck Institute in Leipzig.

At the University of Oslo I lead the Trond Mohn Stiftelse-funded project Algebraic and Topological Cycles in Complex and Tropical Geometries, which consists of members Edvard Aksnes (Ph.D. student), Cédric Le Texier (Ph.D. student) and Matilde Manzaroli (postdoc).

Why did you apply to the Young CAS Fellow programme?

I was interested in the Young CAS Fellow programme because of its focus on collaboration. Many programs for young researchers focus on boosting an individual's body of work, when in reality we rarely work alone, even when we publish solo-authored papers. I appreciate that this program encourages one to strengthen new and established collaborations. It also invites young researchers to branch out into areas that are less familiar, and might be risky, while supported by these collaborations. For example, I hope that my collaborators and I can test out some techniques that have already had an impact in real algebraic geometry in the symplectic world.

What in particular are you looking forward to as a future Young CAS Fellow?

I'm looking forward to bringing people to Oslo in the focused meetings and also using the stretches of time in between. The lengthening of the program to two years makes it very attractive. In any kind of research, changing and challenging perspectives requires time.

See more content from The Centre for Advanced Study:

mathematics natural sciences partner cas centre for advanced study
Powered by Labrador CMS